Online Bass Instruction with Rusty Springfield
The Circle of Fifths

Now for more of that ever-entertaining topic (drum roll please):

Music Theory...

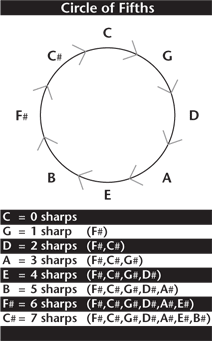
You may be familiar with the term "circle of fifths."

(This does not refer to a backwoods moonshine party in eastern Tennessee. That would be a large "table of fifths" but now we're getting way off topic.)

The "circle of fifths" refers to the fact that, every time you move from one key up a fifth to a new key, you add a "sharp" to the new key. Let's review. The key of C has no sharps or flats. If we move up the interval of a fifth, we come to the key of G, which has one sharp: F#. Go up another fifth and we encounter the key of D, which has two sharps: F# and C#. The next key we come to is A, which has three sharps: F#, C#, G#. You may also notice that the last "accidental" (as sharps, flats, and natural signs are called) in any sharp key is it's seventh degree. Cool huh?


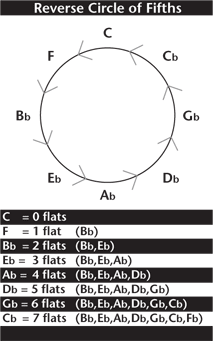All of this begs the question, "How do we derive flat keys?" Glad you asked.

To figure out flat keys, we simply move in the opposite direction. Again, we know that the key of C has no sharps or flats. If we go down a fifth interval from C, we find the key of F, which has one flat: Bb. One more fifth down, and we come to Bb, which has two flats: Bb, Eb. As before, the pattern continues all the way around.
Go to the next lesson: Chords 101